以下是我近期的感悟,该感悟是从被称为辩证法的属世哲学下推导无限存在与量的发生的尝试。我试图分享之。
辩证法与一的法则的联系简述
辩证法对于一的法则而言,或许并不是一个陌生的事物。在古希腊哲学中,就已经有赫拉克利特(一法[25.4]对此有提及)辩证法的萌芽。
赫拉克利特在火本源的观点下,认为“这个世界,对于一切存在物都是一样的,它不是任何神所创造的,也不是任何人创造的;它过去、现在、未来永远是一团永恒的活火,在一定的分寸上燃烧,在一定的分寸上熄灭。”“一切转为火,火又转为一切,有如黄金换成货物,货物又换成黄金。”并通过这样事物之间的相互转化的观念,描述了火、气、水、土四相之间的循环转化。并且基于“一定的分寸”所隐含的规律的观念,在火本源这一“无定形”本源中加入了“有定形”的原则,火是变化无常的,始终处于不断转化的过程中,但其“分寸”、“次序”、“周期”、“必然性”等却是永恒不变的,是世界万物所遵循的普遍法则——这个法则被称为“逻各斯(Logos)”。逻各斯不是外加于火的,而是火本身的固有尺度,它规定和制约着火于万物之间的流变转化,而火又反过来显示出逻各斯的永恒不变性。(邓晓芒《西方哲学史》)
逻各斯(Logos)在一法中,则被描述为"理则"或"爱":
[13.7] 发问者: 在这之后, 发生了什么?
Ra: 这觉察引导到无限的焦点 转入无限能量. 你们曾用各式各样的声音振动复合体称呼这能量, 最常进入你的耳朵的是“理则”(Logos)或“爱”.
在西方哲学的后续发展中,随着古希腊的衰落、罗马的入侵、以及后来欧洲基督教经院哲学的桎梏,辩证法沉寂了相当长一段时间。直到在18世纪活跃的德国古典哲学的开创者康德提出"二律背反",指出对一切事物的不同观点均可以相互冲突、自相矛盾。或许某种意义上来说,康德触及到了第三密度名为"现实世界"之幻象的边界。
该问题有解决,德国古典哲学发展到黑格尔那里,辩证法以黑格尔《逻辑学》的唯心主义形式得到呈现(可以注意到,Logik/Logic与Logos的词根关系)。该思想形态认为,一切悖论/矛盾,都处于对立统一中。于是辩证法有三个规律,对立统一规律、质量互变规律、否定之否定规律,均以正反合(正命题,与之悖论的反命题,两者合一的合命题)命题系统实现。
该思想形态发展到马克思那里,则将"黑格尔的唯心辩证法颠倒了过来",发展成为了唯物辩证法,或者泛称为辩证唯物主义。唯物辩证法帮助马克思建立了唯物史观,主张人类社会阶级的产生、运动(阶级斗争)与阶级的最终消灭,最终人们将从所谓的"必然王国"走向"自由王国",即"人自由而全面的发展"与"自由人的联合体"。除此之外,该思想形态也渗透在了其经济巨著《资本论》(政治经济学批判)中,讨论了商品经济下价值的问题,与剥削奴役人类的资本主义社会自身不可调节的矛盾必然灭亡的规律。
在唯物辩证法后续的发展中,由于它将世界本源问题锚定在所谓的"绝对物质"上,因此造成了唯物辩证法自身的僵化,最终变得庸俗,这集中映现在自由意志的问题上。在马克思那里,人的自由意志即他所谓的"人的主观能动性",马克思本人并非不重视这个问题,然而却也并未对此有过多探讨。而在后续的社会主义实践过程中,人的主观能动性得到践踏,一切都要以教条、领袖、当局或者所谓的"历史的必然"为是,人自身的自由意志终于得到无视。这就是辩证法的悲歌。
因此,辩证法与一的法则的同一性在于,它要求解决矛盾(或者说悖论),将一切置于一个普遍的同一性之下;两者的不同之处在于,辩证法在自由意志的议题上有所混淆(绝对精神,或者绝对物质,都不会导致自由意志)。但是正如辩证法的精神自身宣称所言,事物总是在曲折发展中向着光明前进。让我们重新检视辩证法的合理内核,然后用闪电击打这个高塔吧。
当然,若这个帖子有所干犯论坛准则之第(6)点,请管理员予以提示。我对此始终保持谨慎。
若没有问题,就让我们开始吧。
辩证法的再起征途:存在无限与量的解决
我怀着属灵的美好与和平,向你致意。矛盾有解决,问题有答案,灵魂有力量,现实有希望。我们不会在绝望中死去,我们会在信心中新生。生命的长河一往无前,历史的长河永不终结。我是无人知晓的辽阔黑暗里,万千无名人类中的一个,我们向你分享我们微小、片面的感悟与心得。
1.总述
(日志时间:24年1月2日)
我们讨论存在。我们将从存在的两条普遍规定出发,推导至量的发生。
存在自身( Ding an sich /Ding an sich of Being ) ,或者说任何事物的存在,将导致自身的矛盾。该矛盾有新的进展与解决,将从存在自身中有新的存在构出,这一进展是关系。
关系自身 (Ding an sich of Relationship) 的存在,将会导致自身的矛盾。该矛盾有新的进展与解决,将从关系自身中有新的存在构出,这一进展是性质。
性质 ,或者说质自身(Ding an sich of Quality) 的存在,将会导致自身的矛盾。该矛盾有新的进展与解决,将从质自身中有新的存在构出,这一进展是量。
数量 ,或者说量自身(Ding an sich of Quanity) 的存在,将会导致自身的矛盾。该矛盾有新的进展与解决,将从量自身中有新的存在构出,这一进展是无限的量。无限的量与性质合一,将构成度,或者说维度。我们的讨论将在这里告一段落,但是讨论自身并不会终结。
2.存在
2.1.存在的两条基本规定
(日志时间:24年1月2日)
我们提出两个命题,并建立为存在的基本规定,作为基本假设,或者说基本前提:
| 立论一:事物的存在性
一个事物如果在世界中存在,就意味着它能够与其余事物进行作用。如该事物既不能被观测,也不能对其余事物产生影响,则该事物不存在,或只能存在于世界之外。
| 立论二:事物的独立存在性
一个事物之所以在这个世界中独立存在,是因为它与其它事物产生了区别,或者说差异。
如果一个事物与另一个事物,在任何方面都不存在差异,则这两个事物本来就是一个事物,或者说,这样的事物不存在。
以上两条规定,任何存在都满足,没有反例,因此是普遍的。
2.2.存在自身的矛盾
(日志时间:24年1月2日)
存在自身的矛盾列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 纯存在 | 纯虚无 | 有限存在 |
表1 存在自身的矛盾
2.2.1.存在自身:纯存在,与纯存在走向纯虚无
当一个存在除了满足以上两条存在的基本规定别无其它规定时,称之为存在自身。这样的存在,就是纯存在。
纯存在除了是存在自身之外,便什么都不是。这造成了纯存在自身的矛盾:
(1)由立论一,如果在纯存在(或者说存在自身)之外没有其它存在,否则纯存在不能存在,这违背了存在自身的意义;
(2)如果在纯存在(或者说存在自身)之外还有其它存在,则纯存在并未包括所有存在(以成为存在自身),这同样违背了存在自身的意义。
存在自身,或者说纯存在陷入了这样不可调和的矛盾。
于是,必须要求一个东西与纯存在对立,该存在为纯虚无。
纯虚无不能是任何存在,但是当它作为一个东西与纯存在对立时,其实就已经是一个存在了,该存在除了自身之外,什么存在都不能是,否则违背纯虚无的规定。但是,当作出这样的规定时,纯虚无就已经是纯存在。于是纯存在直接是纯虚无,纯虚无直接是纯存在,彼此同一却互为否定,然而这仍然是矛盾。
因为:纯存在是纯虚无,所以它不是纯存在;因为纯虚无是纯存在,所以它不是纯虚无。这纯粹是概念对概念的粗鄙游戏,但是我们从中看到,无论是纯存在,还是纯虚无,都已经走向了自己的对立面,成为自身所不是。
2.2.2.从存在自身走向有限存在
于是,在这最基本的矛盾中,进一步地,由存在的立论一,有:
纯存在以纯虚无规定自身;同等地,纯虚无以纯存在规定自身。
在这里,双方都取得了一个除了存在之外的意义,那就是由对方的存在导致自身的存在。或者说,一旦自身存在,对方也就必须存在。并且,只要自身一直存在,对方就会一直存在。这就注定了双方要求彼此排斥,而这种差异带来的对立,就是以自身规定对方的存在。
也就是说,两个什么都不是的东西,都自以为是,而把对方看作相对于自身的虚无。对于纯存在来说,自己是全然无缺的存在,对方是什么都没有的虚无。对于纯虚无来说,自己才是那个全然无缺的存在,对方是什么都没有的虚无。双方的地位等同。但正是这样的对立中,互相以自身赋予了对方新的意义。这意义就是——我不是对方,从而自我受限,各自不纯。这样,就从纯存在与纯虚无,走向了一般的存在与虚无,或者说有限存在,从而开始实现。
该实现是:一个存在,既有自身所是(存在),也有自身所不是(虚无)。并且既通过自身所不是规定自身所是,也通过自身所是规定自身所不是。于是矛盾得到解决。该存在即是自身有限,因此是有限存在。存在自身所是与自身不是成为了规定自身的两个方面,于是原先存在与虚无在有限存在的发生上达成了对立统一。
2.2.3.有限存在的导出规定;存在无限
有限存在,由立论二,有:
( 1 )对于任意一个有限存在,其自身所不是,是其它存在自身所是。
该规定有纯存在与纯虚无互相以对方规定自身而来。
一个有限存在,自身所不是的部分(自身的虚无范畴),是其它存在所是(自身的存在范畴)。
于是接着有:
( 2 )对于任意一个有限存在,以其它有限存在规定自身 。
列表如下:

表2 存在的规定进展
在上表的前两个命题系统的正题、反题的二元对立中(第一二列的第二、三行),总有合题的统一(本列第四行;右一列的第一行)。直到存在与存在之间,因为在此处有限存在涉及无限:
( 3 )存在无限 :
对于任意一个有限存在,总有另一个有限存在是其所不是,且对于这两个有限存在所构成的整体而言,仍然有其所不是,并且对所有有限存在总是存在这样的存在。于是存在无限,或者说所有的有限存在构成了无限的存在。( # 注意,这就是证明)
换句话说,存在之外,还有存在,并且这样的存在总是存在,于是所有的存在合称无限存在。此即存在的自为之有。
从这样的无限存在之序列中,有了新的进展,该进展为存在之间的关系。
2.3.差异与无差异;关系
(日志时间:24年1月2日)
关系最初即为存在与存在之间的是与不是的差异。差异存在,并且由每一对存在之间的对立存在,但是不是存在自身(Ding an sich/ Ding an sich of Being),相反地,差异将实现自身,该自身为关系。
任意两个存在之间,都有差异(否则两个存在直接同为一个存在),即有关系。于是接着,存在自身与存在自身之间也有关系,该关系为:没有差异,即差异自身的反题。因此,差异与自身的对立面无差异统一于关系。关系的本质是差异/无差异(所不是 / 所是)。
列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 差异 | 无差异 | 关系 |
表3 差异自身的矛盾
3.关系
3.1.关系自身与普遍联系
(日志时间:24年1月2日)
关系存在,却不是存在自身(Ding an sich/Ding an sich of Being)。
在最初的情况中,关系以存在之间的是与不是(差异与无差异)作为新的进展实现,但是它依附于存在,随着存在的转移而转移,失去了存在,它就不再是自身。因而,没有自身的独立意义,不是一个独立的存在。但是关系存在,因此需要满足存在的立论二,使自身与存在有区别,从而成为关系自身(Ding an sich of Relationship) 。
换而言之,当关系不再以存在的转移为转移时,关系成为了自身。
令有一个无限存在的集合 E ,定义为:
E= {e_1,e_2,e_3,…,e_n,…}
其中,集合 E 中每一个元素 e_i (i=1,2,3,…)都为一个有限存在。
令有一有限存在之间的关系 R ,将关系 R 记为:
R(e_i,e_j)
或图示为:
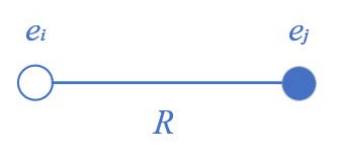
若该关系 R 使得集合 E 中任意一对元素 e_i, e_j ,( i=1,2,3,… ; j=1,2,3,… ;包括元素 e_i 对元素 e_i 自身,即允许有 i=j )都满足,则称该关系 R 为相对于无限存在 E 的关系自身。
该关系 R ,在无限存在 E 的范畴内,将不以任何有限存在的转移为转移,因此成为了关系自身。这一关系 R 对每一对有限存在都作出了规定,于是对无限存在 E 整体有普遍的规定。此为所有有限存在之间的普遍联系。
因此,关系是一个有限存在与另一个有限存在的合题。列表如下(继承自表2 存在的规定进展)。
| 正题 | 反题 | 合题 |
|---|---|---|
| 有限存在自身 | 其它有限存在 | 存在之间的关系 |
表4 存在与关系
该关系自身 R 存在,因为关系的本质是差异/无差异(所不是/所是),这对于所有有限存在是普遍的。但是该关系 R 有自身的矛盾。
3.2.关系自身的矛盾
(日志时间:24年1月2日-3日)
这样的关系自身,除了是关系之外,就不是任何东西,于是是纯关系。它只有空洞的形式,却没有任何内涵,对有限存在没有任何具体的意义。于是与先前的纯存在一般,陷入了困境中。
3.2.1.存在之间差异与无差异的矛盾
这个困境的形式之一为存在之间差异与无差异的矛盾。
对于任意有限存在 e_i ,以及任意另一个不同的有限存在 e_j (i≠j),当纯关系 R 满足:
R(e_i,e_i)
时,则不能满足:
R(e_i,e_j)
因为关系的本质是差异/无差异(所不是/所是),而差异与无差异若直接同一,则意味着:
R(e_i,e_i )=R(e_i,e_j)
e_i=e_j
即 e_i,e_j 为同一个存在,与前提矛盾。
3.2.2 存在之间差异与差异的矛盾
这个困境的形式之二为存在之间差异与差异的矛盾。
对于任意有限存在 e_i ,以及任意另两个不同的有限存在 e_j,e_k (i≠j,i≠k,j≠k) ,当纯关系 R 满足:
R(e_i,e_j)
时,则不能满足:
R(e_i,e_k)
因为关系的本质是差异/无差异(所不是/所是),而 e_i,e_j 之间的差异与 e_i,e_k 之间的差异若直接同一,则意味着:
R(e_i,e_j )=R(e_i,e_k)
e_j=e_k
即 e_j,e_k 为同一个有限存在,与前提矛盾。
3.2.3 关系自身的矛盾
于是,由以上的两个矛盾形式,反映为关系自身的矛盾。
对于任意有限存在 e_i 而言,其与另一有限存在 e_j ( i,j 可以相等或不等)的关系,与再一个有限存在 e_k (j≠k) 的关系,两对关系必然不同,否则必然有两个不同有限存在直接同一的矛盾出现。于是纯关系不纯,必然造成自身的反面以否定自身,于是关系不是无限的,而是有限的。记有限关系为 R_x 。
列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 有关系 R | 无关系 ¬R | 有限关系 R_x (x=1,2,3,…) |
表5 关系自身的矛盾
同样,每一个有限关系,都有自身所是与自身所不是。它反映在:
某一有限关系 R_j ,对于一对存在 e_i,e_j 可能符合,满足:
R_j (e_i,e_j)
对于另一对存在 e_i,e_k (j≠k) 则不符合,但同样有另一有限关系 R_k 可以符合这一对存在的情况,有:
R_k (e_i,e_k)
并且有限关系 R_j 与 R_k 之间有:
R_j≠R_k
于是对于每一对有限存在,都有一个有限关系将它们联系起来。于是有限关系走向无限。
列表如下:
表6 关系的规定进展
于是,与存在无限相对应,所有有限关系合称无限关系,或者说关系的无限存在。
换句话说,关系之外,还有关系,并且这样的关系总是存在,于是所有的关系合称无限关系。此即关系的自为之有。在这里,所谓的普遍联系取得了其真正的实质。
3.3关系之关系;性质
(日志时间:24年1月3日)
3.3.1 矛盾的解决
由于关系取得了有限性的规定,因此,存在之间差异与无差异的矛盾,以及差异与差异的矛盾可以得到解决。
情况如下:
令有限关系 R_i 存在。对于任意有限存在 e_i ,以及任意另两个不同的有限存在 e_j,e_k (j≠k) ,当有限关系 R_i 满足:
R_i (e_i,e_j)
时,可以满足:
R_i (e_i,e_k)
此时不会造成有限存在 e_j,e_k 的直接同一,因为关系 R_i 有限,当 e_j,e_k 共同符合此关系 R_i 时,也只是有限符合,它们在其它方面可以不是同一的,因此存在的差异仍然可以存在。双方在一部分上等同(共同满足某一有限关系),而非直接完全等同(完全满足所有有限关系,以至于双方彼此直接无差别是对方)。
3.3.2 有限存在的同一性
由于关系自身的矛盾得到了解决,并且由于其所造成的关系无限,因此有限存在之间存在有限的同一性。该同一性即为:不同的有限存在可以满足于同一个有限关系。这同一性,将作为一组不同有限存在的共同性质。性质的本质是不同有限存在,在某一有限关系下的同一。
4. 性质
4.1性质自身
(日志时间:24年1月3日)
4.1.1 性质的基本定义
性质自身(Ding an sich of Quality) 是关系矛盾解决的结果。性质的定义如上:性质是不同有限存在,在某一有限关系下的同一。
4.1.2 性质的符号定义
需要注意的是,一个有限关系,仅包含了两个方面的有限存在。因此性质是通过同一个有限存在,去界定其余的不同有限存在是否具有同一性的。我们称这一个性质凭依之同一个有限存在为参照物,或者说参考系的原点。没有参照物,性质无从谈起。
也就是说,对一个有限关系 R_f ,定义某一有限存在 e_f 为其参照物,则当任意两个个有限存在 e_i,e_j (i≠j) 皆满足关系 R_f 时,则称有限存在 e_i,e_j 在关系 R_f 下有同一性。
也即有限存在 e_i,e_j 都符合:
R_f (e_f,e_i)
R_f (e_f,e_j)
当任意两个个有限存在 e_i,e_j (i≠j) 其中一个满足关系 R_f ,另一个不满足时,则称有限存在 e_i,e_j 在关系 R_f 下没有同一性。
由于在这里,有限关系 R_f 与参照物 e_f 都不变,为了方便表达,我们将:
R_f (e_f,x)
其中, x=e_1,e_2,e_3,…
简记为:
f(x)
其中, x=e_1,e_2,e_3,…
由于关系无限,对于无限存在的集合 E ,其中总有一部分有限存在符合有限关系 f(x) (至少有限存在 e_f 本身符合),另一部分有限存在不符合有限关系 f(x) 。于是这将造成性质的判别:
![]()
对于符合关系 f(x) 的有限存在,它们可能是有限个数,也可能是无限个数。记这一组有限存在的集合为 A ,定义为:
A={a_1,a_2,a_3,…,a_n,…}
不难看出, A 是无限存在集合 E 的子集,但是它也可以拥有无限个元素。当集合 A 中的元素不唯一时,则称集合 A 的所有元素有在有限关系下的同一,作为这些元素的共同性质(即同一性)。
对于 ¬A 集合中的所有元素,则称它们没有的性质。
综上所述,性质是一个有限存在 e_f 与一个有限关系 R_f 的合题。列表如下(继承自表4 存在与关系):
| 正题 | 反题 | 合题 |
|---|---|---|
| 有限存在 e_f | 有限关系 R_f | 性质 f(x) |
表7 存在、关系与性质
4.2性质的矛盾;量自身
(日志时间:24年1月3日)
从以上讨论中,不难看出,性质已经是有限的。但是为了格式的一致性,仍然列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 有性质 | 无性质 | 有限性质 f(x) |
表8 性质自身的矛盾
这并非没有矛盾,而是矛盾造成了必须的新的进展。性质有自身所是,也有自身所不是,这直接造成了新的进展发生。该新的进展就是判断出的东西:
![]()
这个判别式判出的右侧的东西,既不是存在自身,也不是关系自身,也非性质自身,它是一种新的进展。性质的是与不是,由该进展的表出解决。该进展就是通过既定参照物 e_f 对其它存在的判别,或者说对有限存在最初的衡量。该衡量产生了两种结果的存在,符合或不符合(是或不是)。此即最初的量,或者说量自身。
5. 数量
5.1量自身的矛盾
(日志时间:24年1月3日)
量自身是有限性质矛盾的新进展。量自身的存在,同样有自身的矛盾。对任意一个有限存在的性质判别,无非就是两个对立的结果,存在性质(符合关系)或不存在性质(不符合关系)。判断结果的“存在”即纯量,或者说量自身(Ding an sich of Quanity) 。
该量是某个有限存在在判断式(性质)下的反映,因此必然不是性质自身,而是从性质中映出的东西(新的进展)。它必然不是性质,也不是关系,也不是存在(它也只是存在的一个反映,而非存在自身(Ding an sich of Being)),所以它只能是新东西。
与这个东西同时出现的是它的对立面,或者说它的否定,也就是判断的另一个结果“虚无”(性质不满足;关系不存在),该对立面即为无量。
纯量与无量,作为此时的“纯存在”与“纯虚无”(当然,这只能是纯存在与纯虚无的映射,因为此时它是量自身(ding an sich of Quanity),而非存在/虚无自身),将会再一次发生关系,否则将会面临曾经的纯存在与纯虚无都因为除了自身之外别无意义(从而不是自身)的情况。
于是从量自身的纯量/无量(一个有限存在,一个有限性质的合题)过渡到了限量(一个有限关系,一个有限性质的合题),这是必然的结果。
列表如下(继承自表7存在、关系与性质):
| 正题 | 反题 | 合题 |
|---|---|---|
| 有限存在 | 有限性质 | 量自身(纯量/无量) |
表9 存在、性质与量自身
| 正题 | 反题 | 合题 |
|---|---|---|
| 有限关系 | 有限性质 | 限量 |
表10 关系、性质与限量
| 正题 | 反题 | 合题 |
|---|---|---|
| 纯量 | 无量 | 限量 |
表11 量自身的矛盾
5.2有限的量与无限的量
(日志时间:24年1月3日)
5.2.1 限量的意义
限量的意义是:
(1)在同一质上,任意一个限量的存在,既有自身所是,又有自身所不是,缺失了任何一个方面,该量的存在都不再完整,于是退回到纯量/无量的范畴中,但是很遗憾没办法退回去。
也就是说,在同一质上,限量由量自身与自身所不是共同规定。参见表11 量自身的矛盾。
(2)任何一个限量,都与其它限量不同,若相同,则同为一个限量,于是违背了存在的立论二:独立存在性。因此不同两个限量之间有彼此所不是的关系,不同的两个限量之间的关系,即为差异。
列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 差异 | 关系 | 限量规定下的差异(量差) |
表12 差异自身矛盾的再现
(3)差异反映在每一个限量自身所不是的范畴:一个限量的自身所不是,可以是其它限量所是。
(4)在同一质上,每一对限量,都有同一性质作为彼此的同一性。因此,对于每一对不同的限量,都既有同一的部分,又有不同(差异)的部分。
性质作为同一性的意义是:每个限量都包含着纯量(它是性质的直接结果),也就是说,在每一个限量中,任意纯量都要存在,否则脱离了同一质的意义,于是此时纯量取得了限量的规定,该规定为无穷小/微元——在任意限量中都存在。于是该纯量可以在每一份限量中存在,并且实现自身为自为之有。
5.2.2 无穷小与0
满足某一性质 f(x) 的有限存在,无论其多么微弱,它始终在该性质下存在,于是映射为量,这一量无论是什么样的限量,都必然包含包含一份微元。换句话说,所有满足性质 f(x) 的有限存在所映出的量都含有无穷小的微元。
也就是说,每一份限量的微元,或者说无穷小,其实反映了性质 f(x) 自身。微元或者无穷小即性质在量上的反映(微元或者无穷小接纳一切满足此性质的有限存在),而不符合性质 f(x) 的有限存在,则在该映射下映出为 0 。
综上所述,纯量被限量所规定为无穷小,无量被限量所规定为 0 。
因此,可以将性质 f(x) 的判别式:
![]()
转写为:

接着可以直接看到纯量与无量的对立统一:无穷小趋近于 0 (量的不存在/无量的量),从而纯量/无量都不再是原来的自己,而是通过限量之扬弃而对立统一了。
5.2.3 无穷大;无限的量
定义限量的符号为 y_i (i=1,2,3,…) 。
对于限量,由于限量的意义之(3)、(4)点,一对不同的限量 y_i 与限量 y_j (i≠j) 的基本关系判断为:对于任意限量 y_i 自身所不是的范畴,总有另一个限量 y_j 在该范畴所是,并且由于限量的同一性,该限量 y_j 自身所是包含了限量 y_i ,并且该限量 y_j 同样有自身所不是。
定义这两个限量之间的差异为 Δy_{ij} ,该 Δy_{ij} 即是 y_i 所不是,却是 y_j 所是,则对于任意两个不同的限量 y_i 与 y_j ,总有关系:
y_j=y_i+Δy_{ij}
或作图表示:
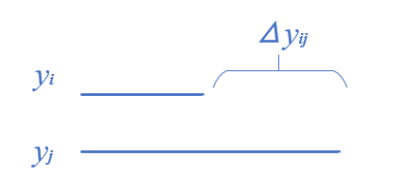
该关系通过差异 Δy_{ij} 实现,或者说该关系的本质就是差异。
这实质上就在质上构成了大小关系,对于全部限量而言,都满足此关系。所以,对于任意一个非 0 限量,都有比自身更小者,也有比自身更大者,并且这样的大小关系总是可以存在。于是限量从整体上而言构成了无限的量,一方面直到无穷小,另一方面直到无穷大。所有的限量合称无限的量。此即量的自为之有。
列表如下:
| 正题 | 反题 | 合题 |
|---|---|---|
| 量自身 | 限量 | 无限的量 |
表13 量的矛盾解决
由于无限的量这样的无限合称性,因此每一对限量彼此之间既是连续的,也是离散的,在这里我们不想再多区分,直接照抄黑格尔对量的连续与离散的论述即可。
受到量的自为之有规定的性质 f(x) ,此时的判别表达式不再是二元对立的,而是连续的。也就是说,的判别式:

进一步转形为:
f(x)=y
y∈R^+∪{0},其中, R^+ 为正实数集。
于是性质也成为自为之有。质与量的对立统一构成了维度。
对之前的讨论进行列表回顾:
表14 量的解决
表15 质/量的进展
6. 维度
(日志时间:24年1月3日)
维度是性质与无限的量的合题。一个维度,包含了一个性质与一个无限的量。
| 正题 | 反题 | 合题 |
|---|---|---|
| 性质 | 无限的量 | 维度 |
表16 性质、无限的量与维度
维度有限。该有限不能是限量的有限,因为已经处于无限的量的规定中。因此无法用一个维度去包含另一个维度(这结果还是同一个维度)。于是每一对有限维度之间都必须是分离的。
该有限的分离性产生于性质在量上无穷小的定义。每一个性质只能在量上作为无穷小存在,它是维度的正题,因此维度也服从这一规定。因此有限维度之间在量的无穷小处对立统一,该对立统一的实质是垂直关系。
该垂直关系的对立统一,将构成空间。读者有兴趣可以自行思考。


